Polygonal Slip Surface
The solution of the slope stability problem adopting the polygonal slip surface is based on the determination of the limit state of forces acting on the soil body above the slip surface. To introduce these forces the slip surface above is subdivided into blocks by dividing planes. Typically, these planes are assumed vertical, but this is not a required condition, e.g. the Sarma method considers generally inclined planes.
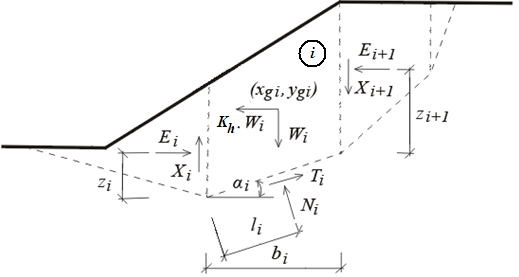 Static scheme of block
Static scheme of block
The figure shows forces acting on individual blocks of soil. If the region above the slip surface is divided into blocks, then for the evaluation of unknowns we have: n normal forces Ni acting on individual segments and corresponding n shear forces Ti; n-1 normal forces between blocks Ei and corresponding n-1 shear forces Xi ; n-1 values of zi representing the points of application of forces Ei, n values of li representing the points of application of forces Ni and one value of the factor of safety SF. Forces Xi can be in some methods replaced by the values of inclination of forces Ei.
To following set of equations is available to solve the problem of equilibrium: n horizontal, and n vertical equations of equilibrium written for individual blocks, n moment equations of equilibrium for individual blocks and n relations between Ni and Ti forces developed on blocks according to the Mohr-Coulomb theory. In total there are 4n equations for 6n-2 unknowns. This suggests that 2n-2 unknowns must be chosen a prior. Individual methods differ from each other in the way these values are selected.
Most often points of application of individual forces acting between blocks or their inclinations are selected. Solving the problem of equilibrium it proceeds in an iterative manner, where the selected values must allow for satisfying both the equilibrium and kinematical admissibility of the obtained solution.
The program allows for adopting one of the following methods:
Optimization of polygonal slip surface searches the most critical surface (the lowest safety factor SF).