Drucker-Prager
The model requires inputting the following parameters: modulus of elasticity E, the Poisson's ratio, angle of internal friction and cohesion. The latter two parameters serve to define the yield condition. The formulation of constitutive equations assumes effective parameters of angle of internal friction φeff and cohesion ceff. The angle of dilation must also be specified.
The Drucker-Prager model (sometimes also known as the extended von Mises model) modifies the Mohr-Coulomb yield function to avoid singularities associated with corners. Unlike the Mohr-Coulomb model the Drucker-Prager yield surface is smooth and plots as a cylindrical cone in the principal stress space. Similarly to the MC model the DP yield surface depends on the effective mean stress σm. The current version of the DP model implemented in FEM builds upon the assumption of triaxial extension. In other words, the yield surface projection into the deviatoric plane touches the inner corners of the Mohr-Coulomb hexagon (θ = -300), where θ is the Lode angle.
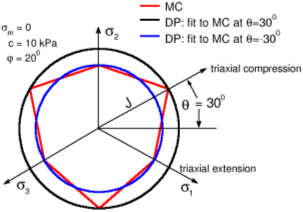 DP and MC yield surfaces in the deviatoric plane
DP and MC yield surfaces in the deviatoric plane