Modelo de materiales en el análisis de flujo
El análisis de flujo de estado estacionario se lleva a cabo por la ley de Darcy especificando las relaciones entre la velocidad del flujo y el gradiente de la cabeza hidráulica. La versión actual del programa asume valores constantes de coeficientes de permeabilidad independientes de la presión de poros.
El programa además requiere que se especifique el índice vacío inicial e0 para la determinación de la porosidad actual n y subsecuentemente la velocidad actual del agua fluyendo entre los poros solo vs=v/n, donde v es el promedio de la velocidad de agua en toda la zona. Generalmente, el índice vacío e0 = 1 corresponde a suelos con porosidad de n = 50%
Por el ingreso del coeficiente de permeabilidad relativa Kr el programa permite el seguimiento de la zona de transición entre regiones completamente saturadas (S = 1, Kr = 1) y regiones no saturadas (Kr => 0) del cuerpo del suelo. Como un ejemplo se puede considerar el problema de flujo no confinado.
El proceso de seguimiento de zona de transición se lleva a cabo por uno de los tres modelos de zona de transición determinando la evolución de coeficientes de permeabilidad relativa Kr como la función de cabecera de presión de poros, ver figuras.
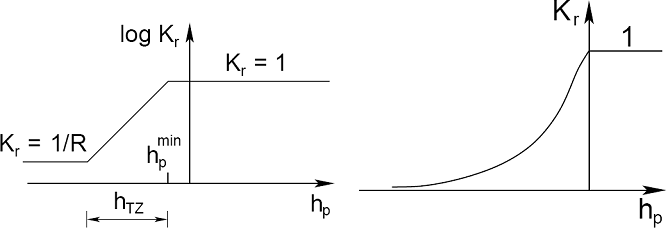 (a) Modelo log-linear [1], (b) Modelo Van Genuchten [2]
(a) Modelo log-linear [1], (b) Modelo Van Genuchten [2]
Modelo log linear
La zona de transición del modelo log linear descripta por ejemplo en [1] se define por los siguientes parámetros:
hpmin | mínimo valor de cabeza de presión en una región completamente saturada [kPa] | ||
hTZ | - | Ancho de la zona de transición [m] | |
R | - | Parámetro de reducción, un número suficientemente largo R = 100-1000 [-], por defecto asume R = 1000 [-] |
El coeficiente de permeabilidad relativa Kr está dado por:
![]()
Modelo Gardner
Este es un modelo equivalente dependiendo de un solo parámetro α [1/m]. El coeficiente de permeabilidad relativa Kr esta en este caso dado por:
![]()
Modelo Van Genuchten
En este caso el valor de coeficiente de permeabilidad relativa Kr está dado por:
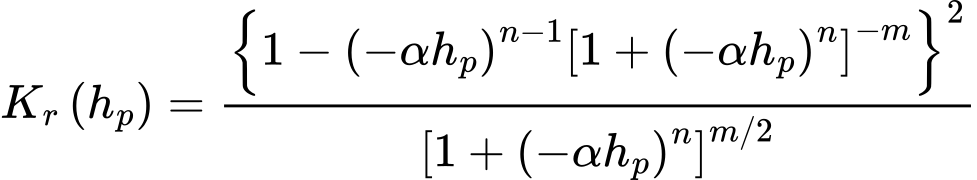
donde α [1/m], n > 1, m = 1 - 1/n son parámetros modelo. Sus valores pueden obtenerse de mediciones de laboratorio de curvas de retención aproximadas por:
![]()
![]()
Donde: | Ssat | - | grado de saturación de un suelo totalmente saturado, configuración por defecto Ssat = 1 |
Sr | - | grado de saturación residual | |
Θ | - | contenido de agua normalizado |
Parámetro Θ está en general dado por:
![]()
Donde: | θr | - | contenido de agua residual [m3/m3] |
θS | - | contenido de agua de un suelo totalmente saturado [m3/m3] |
El grado de saturación actual S puede ser expresado como la proporción del contenido de agua θ y porosidad n como sigue: (es necesario distinguir entre n que representa la porosidad y n, que aparece en el modelo Van Genuchten que se trata de otra variable diferente).
![]()
Los modelos Log-linear y Gardner adoptan una versión simplificada del modelo Van Genuchten según [5]:
![]()
donde b > 0 [-] es un parámetro de ajuste que permite una mejor aproximación de los datos de retención de un suelo dado.
Le recomendamos la siguiente tabla de parámetros que se utilizan actualmente en el programa. Estos parámetros derivan de los indicados en las tablas originales.
Los valores óptimos de los parámetros del modelo de Van Genuchten para diversas clasificaciones basadas en USDA y FAO y se presentan en las siguientes tablas.
Tabla con coeficientes de regresión para tamaño de grano USDA según Van Genuchten (1991)
Suelo (tamaño de grano) | Ksat [m/day] | RETC | Rosetta | ||||||
e [-] | Sr [-] | α [1/m] | n [-] | e [-] | Sr [-] | α [1/m] | n [-] | ||
Arena | 7,13 | 0,75 | 0,11 | 14,5 | 2,68 | 0,60 | 0,14 | 3,5 | 3,18 |
Arena arcillosa | 3,50 | 0,70 | 0,14 | 12,4 | 2,28 | 0,64 | 0,13 | 3,5 | 1,747 |
Marga arcillosa | 1,06 | 0,70 | 0,16 | 7,5 | 1,89 | 0,63 | 0,10 | 2,7 | 1,448 |
Marga | 0,25 | 0,75 | 0,18 | 3,6 | 1,56 | 0,66 | 0,15 | 1,1 | 1,474 |
Limo | 0,06 | 0,85 | 0,07 | 1,6 | 1,37 | 0,96 | 0,10 | 0,7 | 1,677 |
Marga limosa | 0,11 | 0,82 | 0,15 | 2,0 | 1,41 | 0,78 | 0,15 | 0,5 | 1,663 |
Marga arcillosa de arena | 0,314 | 0,64 | 0,26 | 5,9 | 1,48 | 0,62 | 0,16 | 2,1 | 1,33 |
Marga arcillosa | 0,062 | 0,70 | 0,23 | 1,9 | 1,31 | 0,79 | 0,18 | 1,6 | 1,415 |
Marga arcillosa limosa | 0,017 | 0,75 | 0,21 | 1,0 | 1,23 | 0,93 | 0,19 | 0,8 | 1,52 |
Arcilla arenosa | 0,029 | 0,61 | 0,26 | 2,7 | 1,23 | 0,63 | 0,30 | 3,3 | 1,207 |
Arcilla limosa | 0,0048 | 0,56 | 0,19 | 0,5 | 1,09 | 0,93 | 0,23 | 1,6 | 1,321 |
Arcilla | 0,048 | 0,61 | 0,18 | 0,8 | 1,09 | ||||
Tabla con coeficientes de regresión para tamaño de grano FAO según Van Genuchten (1998)
Suelo (tamaño de grano) | Ksat [m/day] | e [-] | Sr [-] | α [1/m] | n [-] |
Superficie del suelo (profundidad de 1 m) | |||||
Grueso (C) | 0,600 | 0,68 | 0,062 | 3,83 | 1,3774 |
Mediano (M) | 0,121 | 0,78 | 0,023 | 3,14 | 1,1804 |
Fino mediano (MF) | 0,023 | 0,75 | 0,023 | 0,83 | 1,2539 |
Fino (F) | 0,248 | 1,08 | 0,019 | 3,67 | 1,0120 |
Muy fino (VF) | 0,150 | 0,78 | 0,016 | 2,65 | 1,1033 |
Superficie del suelo (profundidad > 1 m) | |||||
Grueso (C) | 0,700 | 0,58 | 0,068 | 4,30 | 1,5206 |
Mediano (M) | 0,108 | 0,65 | 0,026 | 2,49 | 1,1689 |
Fino mediano (MF) | 0,040 | 0,70 | 0,024 | 0,82 | 1,2179 |
Fino (F) | 0,085 | 0,93 | 0,021 | 1,98 | 1,0861 |
Muy fino (VF) | 0,082 | 1,17 | 0,019 | 1,68 | 1,0730 |
Tabla: Sistema de clasificación de la textura del suelo de FAO
Suelo | Definición |
Grueso (C) Mediano (M) | arcilla < 18% y arena > 65% 18%< arcilla < 35% y 15%< arena o: arcilla < 18% y 15%< arena < 65% |
Fino mediano (MF) | arcilla < 35% y arena < 15% |
Fino (F) | 35%< arcilla < 60% |
Muy fino (VF) | 60%< clay |
Bibliografía:
Más detalles se encuentran en [2].
[1] D.M. Potts, L. Zdravkovič, Finite element analysis in geotechnical engineering – theory, Thomas Telford, London, 1999.
[2] M. Th. Van Genuchten, A closed formulation for predicting the hydraulic conductivity of unsaturated soils, Journal Soil Science Society of America 44, 239-259, 1988..
[3] M. Šejnoha, Finite element analysis in geotechnical design, to appear (2013)
[4] W. R. Gardner, Some steady-state solutions of the unsaturated moisture flow equation to evaporation from a water table, Soil Science 85(4), 228–232, 1958.
[5] M. Šejnoha, T. Janda, H. Pruška, M. Brouček, Modelování geotechnických úloh metodou konečných prvků: Teoretická základy a aplikace, předpokládaný rok vydání (2014)
[6] USDA 1951. Soil Survey Manual. Soil Conservation Service. U.S. Department of Agriculture Handbook No. 18. US Government Printing Office. Washington DC.
[7] Wösten, J.H.M., et. al. 1998. Using existing soil data to derive hydraulic parameters for simulation models in environmental studies and in land use planning. Final Report on the European Union Funded project. DLO Winand Staring Centre. Report 156, Wageningen, NL. p. 106. ISSN 0927-04537.